Convex Hull Readme

flash application by Christopher Salvarani

What does the program do?

The program finds the convex hull of a set of points inputted by the user. It walks through the algorithm showing each step.

How do I run the program?

You run the program by opening the convex.html file. It will load the HTML page which embeds the flash program.

What is the input?

The input is a set of points. The user clicks various spots on the screen to input the points, and then when ready clicks the appropriate buttons on the bottom bar.

How does Chan's algorithm work?

Here is the pseudocode for Chan's algorithm:

Input: P∈ℝ² : |P|=n>0

For m = 2; ; m = MIN(n,m²)

	Partition P into P0,P1,...,Pq where |Pi|=m for all i<q and |Pq|>0

	Run an O(nlogn) convex hull algorithm on each Pi. Let CHi be the convex hull of Pi

	Find leftmost point in P, call it left

	Initialize output to empty stack (we refer to the top of the stack as output0)

	output.push(left)

	Repeat m times

		For each CHi, find the point in CHi which is rightmost from output0, call it ri

		Find the point in {r0,r1,...,rq} which is rightmost from output0, call it right

		if left = right, return output

		output.push(right)

Chan’s algorithm works by guessing h (the number of points on the convex hull) to be m (initial guess of 2 is acceptable), and then dividing the set of points into O(n/m) subsets of O(m) points and computing the convex hull of each of these with an O(nlogn) algorithm (like Graham scan). This takes O(nlogm).

It then uses a variation of Jarvis march (a naïve O(nh) convex hull algorithm) in conjunction with the already computed convex hulls to construct the convex hull. Jarvis march is sped up to O(nlogm) using the pre-computed mini-hulls, which we can search using a variation of binary search. If the value for m guessed was too low (we figure this out when we take m steps and have not returned to the starting vertex), we bail out and try a greater value for m (the square of m) without exceeding n.

What is the running time of Chan's algorithm?

Each iteration of Chan's algorithm has a running time of O(nlogm)

Partitioning P takes O(n).
Finding the convex hull of a single partition takes O(mlogm), and we do it O(n/m) times. So, this takes O(nlogm).
Finding the leftmost point in P takes O(n).
Finding the rightmost points in each partition takes O(n/m*logm) (O(logm) for each using binary search on the convex hull). Finding the rightmost of these takes O(n/m), so O(n/m*logm) dominates. We repeat this m times, so this takes O(nlogm).

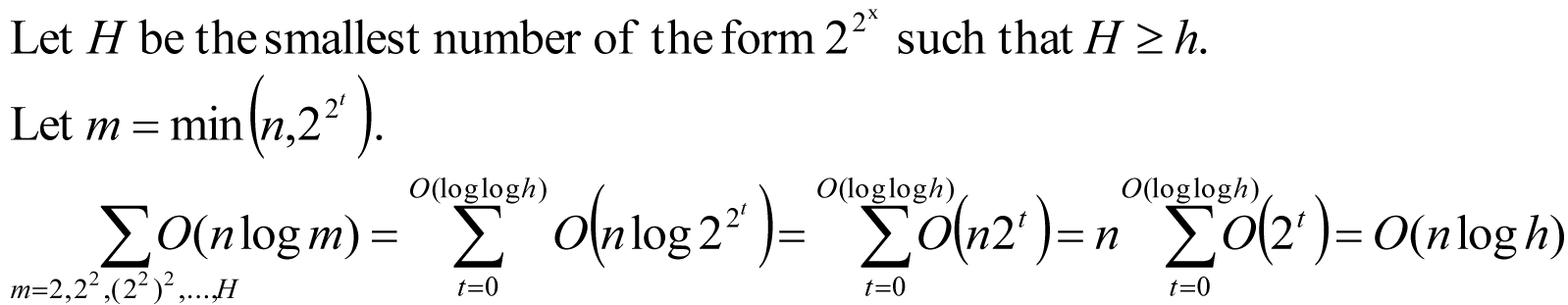
Summing over each iteration gives us (notice that the summation simplifies to a geometric series, which is bounded as shown):

So, Chan’s algorithm has an overall running time of O(nlogh).